幸福は「遺伝」と「環境」のどちらで決まるのか？

皆さんは、『幸せ』は何によって決まると思いますか？

例えば、人には持って生まれた素質というものがあります。容姿といった身体的特徴、運動能力や知的能力、さらには体質など、「遺伝」の影響が大きいとされる要素はたくさんありますよね。これらの要素が、これまでの自分の人生や生活に影響してきただろうことは、皆さんも思い当たる経験があるのではないでしょうか。

一方で、私たちの生活や人生は、自身を取り巻く環境からも影響を受けると考えられます。家庭環境、学校・職場といった社会的なつながり、住んでいる地域、経済状況など、私たちは日々さまざまな「環境」の中で生活しています。

では、この「遺伝」と「環境」は、人の『幸せ』にどのような影響を与えているのでしょうか？

「遺伝」と「環境」に関する研究は様々なものがありますが、今回はAI × ウェルビーイングというテーマで、2024年に学術誌 Nature Mental Healthに掲載された研究を紹介したいと思います。

この研究では、成人期のウェルビーイングを予測する機械学習モデルを構築し、そのモデルを解析することで、「遺伝」や「環境」といった要素がモデルの予測精度に与える影響について調査しています。

対象とするウェルビーイング：主観的幸福

「ウェルビーイング」と一言で言っても、実際にはさまざまな定義や概念があります。

大きくは、主観的幸福（Subjective Well-Being）と心理的幸福（Psychological Well-Being）の二つに区別されますが、これらを統合した複合的な概念を一般的に「ウェルビーイング」として総称することが多いのです。

• 主観的幸福：人生に対する満足度といった、認知的・感情的な幸福感
• 心理的幸福：成長や自己実現、人生の目的といった、より深い次元の幸福感

この研究では、データ上の関係から「主観的幸福」の方に焦点を当てています。具体的には、生活満足度尺度 (Satisfaction with Life Scale)、主観的幸福度尺度 (Subjective Happiness Scale)、キャントリルの梯子 (Cantril Ladder)の3つの尺度をもとに、総合的なウェルビーイングの連続スコアを定義し、目的変数として活用しています。

なお、これらウェルビーイング尺度の種類については、別記事でのまとめもありますので、気になる方はそちらもご参照ください。

幸福度測定の近代史

実験データ：双子の長期間追跡データを活用

利用データは、オランダ双生児登録にて1991〜2022年の間に収集された、幼少期から成人期までの個人単位の追跡データです。
（なお、こういった遺伝と環境に関する研究では、双子のデータがよく利用されます。一卵性双生児だと遺伝子が100%同一のため、純粋に環境要因を分離して評価できるなど、様々なメリットがあるためです。）

このデータは特徴として、幼少期から成人期にかけて2〜3年毎にデータを収集しているため、成人期のウェルビーイング予測に幼少期からの長期的影響も含めて調査を行った点が、この研究の新しさの一つといえます。

特徴量：3つのカテゴリ

この研究で活用する特徴量は、「遺伝」「客観的環境」「主観的環境」の3つのカテゴリに分類されます。

※ 論文内ではそれぞれ、ゲノム(Genome)、一般エクスポソーム(General Exposome)、特定エクスポソーム(Specific Exposome)と表記されていますが、本記事ではイメージしやすい表現に変換しています。

個人の幸福感は、遺伝と環境による多様な要素が、複雑かつ長期的に相互作用することで影響を受けるものと考えられます。そのため、これら情報を組み合わせたマルチモーダルな予測を試みたことが、本研究の最大の特徴といえます。

	遺伝	客観的環境	主観的環境
データの出所	ゲノムワイド関連解析（GWAS）	公的データベース	自己報告（個人および親アンケート）
範囲	遺伝的リスクや傾向	地域の物理的・経済的環境	心理社会的要因、家庭環境
データ例	ポリジェニックスコア（身体特性など）	緑地面積、住宅価格、空気汚染など	孤独感、楽観主義、運動習慣など

1. 遺伝

遺伝の特徴量には、ポリジェニックスコアと呼ばれる数値が利用されています。簡単に言うと、私たちの身体にはDNA配列という形で遺伝情報が記録されていますが、この配列には人それぞれわずかな違いがあります。このわずかな違いが、身長や性格といった形質にどの程度影響を与えるのかは、ゲノムワイド関連解析（GWAS）によって統計的に調査されています。そのため、個人のDNA配列を調べることで、その人物が特定の形質について遺伝的影響を受けやすい傾向にあるかを推定できるのです。この傾向を数値として表したものが、ポリジェニックスコアです。

例えば、あなたが「BMI」という形質のポリジェニックスコアが高かった場合、あなたは遺伝的に太りやすい傾向にあることが分かるのです。

この研究の特徴量が対象としている形質は、例えば以下などが挙げられます。

• 身体的特性・成長（身長、BMI、頭囲、思春期の成長速度、等）
• 精神疾患・行動（ADHD、不安障害、強迫性障害、双極性障害、等）
• 心理社会的特性（協調性、外交性、レジリエンス、孤独感、等）
• 健康・生活習慣（運動習慣、喫煙、飲酒、等）

2. 客観的環境と主観的環境

客観的環境は、例えば空気汚染や住宅価格といった、人口・集団レベルで曝される環境に関する情報です。生まれ育った街や生活エリアにおける、周囲の物理的・経済的環境を表す客観的指標に基づいており、対象者の郵便番号をもとに公的データベースなどから収集されました。

一方で、主観的環境は、例えば性格特性や社会的つながりの有無といった、個人レベルの環境に関する情報を指しています。こちらは本人や親へのアンケート調査による自己申告に基づいており、家庭環境や友人関係といった、より主観的な環境情報となっています。

それぞれの具体例は、以下などが挙げられます。

• 客観的環境：
  • 自然環境（空気汚染、緑地・公園面積、都市比率、等）
  • 経済・インフラ（世帯収入の中央値、公共施設の密度、等）
  • 地域構成（近隣の人口分布、民族構成、等）
• 主観的環境：
  • 心理的要因（楽観主義、孤独感、精神的健康状態、等）
  • 社会的要因（家族や友人からの支援、信頼できる友人の有無、等）
  • 育児や家庭環境（両親の運動習慣、子どもに対する教育方針、等）

予測モデル構築：スタッキングを活用

ウェルビーイング予測には、回帰モデルが構築されています。先行研究に基づいて、スタッキング¹と呼ばれるアンサンブル学習手法を採用しており、ベースモデルの予測結果をメタモデルで統合することで精度向上を図っています。

• ベースモデル：
  • XGBoost (勾配ブースティング)²
  • SVM (サポートベクターマシン)³
  • RF (ランダムフォレスト)⁴
• メタモデル：
  • XGBoost (勾配ブースティング)

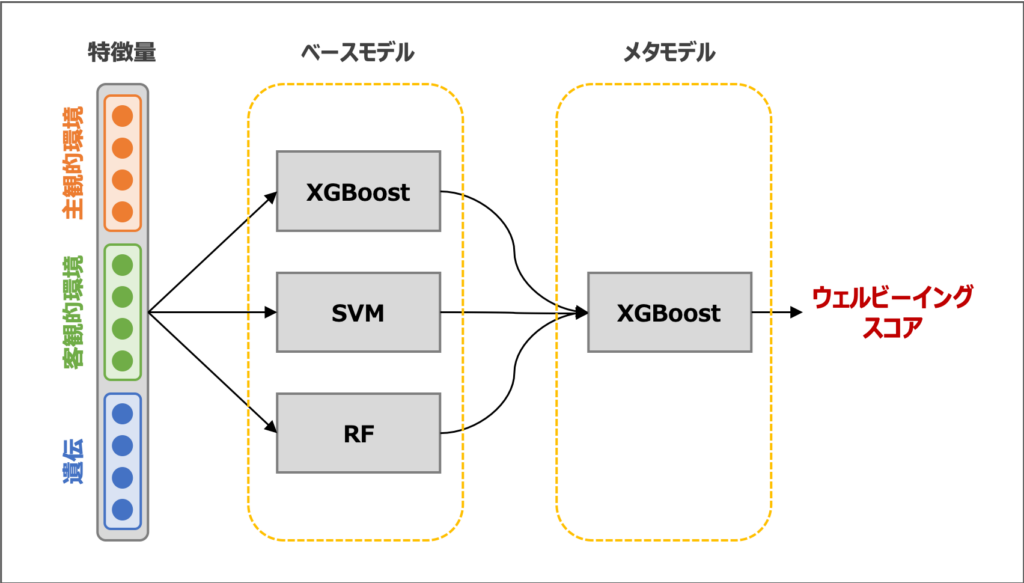
また、予測精度に重要な影響をもつ特徴量を、SHAP値⁵とPermutation Importance⁶を用いて調査しています。どちらも特徴量の重要度を定量化する手法であり、これにより論文著者らは『幸せ』にとって重要な要因を探っていきました。

実験結果：遺伝よりも環境の影響が大きい

1.「主観的環境」がウェルビーイング予測に効果的

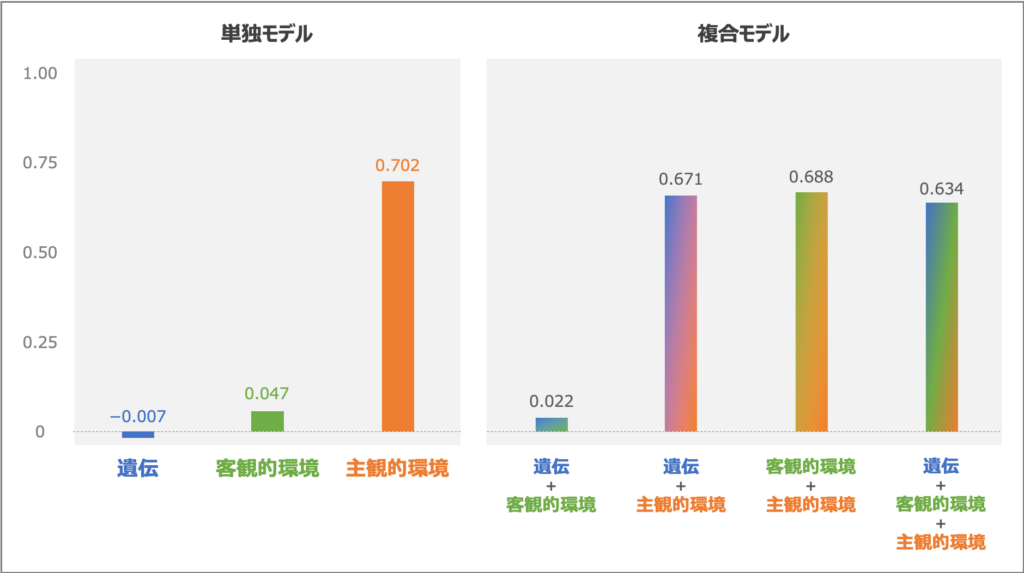
実験の結果、「主観的環境」が予測精度に大きく貢献することが分かりました。
上図は、「遺伝」「客観的環境」「主観的環境」の3つをそれぞれ単独で特徴量に用いたモデル（左）と、組み合わせた複合モデル（右）を、性能比較したものです（評価指標＝決定係数R²⁷）。

単独モデルのほうでは、「主観的環境」を特徴量に用いたモデルが、他2つを圧倒する性能を見せています。これはつまり、「主観的環境」がウェルビーイング予測に最も効果的であり、一方で「遺伝」や「客観的環境」はほとんど寄与していないということです。（ただし「客観的環境」モデルは、小さいが有意な予測力を示しました。）

複合モデルの方では、組み合わせパターンを変えたどのモデルであっても、「主観的環境」の単独モデルと同等か低い性能しか示しませんでした。「遺伝」や「客観的環境」との相互作用が反映されてモデルの性能が向上するかと想像しましたが、相互作用による性能向上は起きなかったようです。

2. 楽観的思考や人間関係が最重要！

では、「主観的環境」の一体何が、ウェルビーイング予測の精度向上に効いていたのでしょうか？
以下の表は、単独モデルにおいて重要度が高かった特徴量の一部を整理したものです。

カテゴリ	ドメイン	特徴量	取得時期
主観的 環境	楽観主義	将来に対する楽観性	成人期 （平均27歳）
	楽観主義	良いことがめったに起きないと感じる	成人期 （平均27歳）
	楽観主義	悪いことよりも良いことが多いと期待する	成人期 （平均27歳）
	孤独感	めったに孤独・憂鬱を感じない	成人期 （平均18歳）
	孤独感	交友関係が不足していると感じる	成人期 （平均21歳）
	孤独感	孤独を感じる	成人期 （平均21歳）
	性格特性 （外交性）	明るく元気な人間だ	成人期 （平均21歳）
	性格特性 （外交性）	自分を「軽薄な人間 」だと思っていない	成人期 （平均18歳）
	精神的健康	自分は無価値だと感じる	成人期 （平均27歳）
	精神的健康	空虚に感じる	成人期 （平均21歳）
	健康	健康状態の自己評価	成人期 （平均27歳）
	社会的関係	親密な関係の有無	成人期 （平均18歳）
	運動	親がスポーツを行っている	幼少期 （10歳）

「主観的環境」では、特に成人期における特徴量が大半を占めていて、楽観主義・孤独感といった心理社会的要因や、外向性といった性格特性が『幸せ』に大きく影響していることが分かりました。大人になってからも、未来に明るい希望を抱き、周りの人とのつながりを大切にすることが、本人の幸福感に重要であることが示唆されていますね。

一方で、幼少期における特徴量として唯一、「10歳前後の親の運動習慣」が高い重要度を示しており、親が運動をする家庭の子どものウェルビーイングは向上しやすいという、面白い傾向も判明しています。

カテゴリ	ドメイン	特徴量	取得時期
客観的 環境	収入	複数世帯の住宅所得	幼少期 （10歳）
	住宅 ストック	新規建設住宅数	幼少期 （12歳）
	住宅 ストック	住宅取引数	幼少期 （10歳）
	住宅 ストック	住宅用不動産の改築件数	幼少期 （10~12歳）
	住宅 ストック	アパート取引数	幼少期 （10歳）
	アメニティ	スイミングプールの数	成人期 （平均21歳）
	教育	中等教育から成人中等教育への進学者数	成人期 （平均18歳）

また、「客観的環境」の特徴量にも、いくつか重要な傾向がありました。注目すべきは、住宅ストックに関する特徴量が多いことと、幼少期における特徴量が大きな割合を占めていることです。子どもの発達にとって重要な時期に、生活している住宅環境・地域経済が安定していることが、将来のウェルビーイングに好影響を及ぼすことが示唆されています。

まとめ

• 「主観的環境」が最も重要であり、ウェルビーイング予測に寄与する。特に成人期における、楽観主義などの心理特性や社会的つながりが重要な予測因子。
• 「客観的環境」の効果は限定的だが、幼少期の住宅環境や地域経済の関連指標が最も強い影響力を持つ。
• 「遺伝」の影響は非常に小さく、ウェルビーイングの予測に寄与しない。

論文著者らは、「客観的環境」や「遺伝」の効果が低かった理由の一つとしてデータ的限界を挙げており、詳細なデータ取得を今後の課題としています。また、利用データがオランダ国内限定のため、グローバルでも同様の傾向があるとは必ずしも断言することはできません。

一方で筆者としては、今回の結果はかなり前向きな解釈ができる印象を受けました。ウェルビーイングに影響するのは、遺伝や周囲環境といったコントロールできない要素ではなく、個人の心の持ち様によって決まると言えるため、誰でもトレーニング次第で『幸せ』を高めることができると考えられます。また、良好な人間関係を持って孤独を遠ざけることが重要であると、改めて認識できる結果でありました。

弊社のサービスでも、心の前向きさ・同僚とのつながりをつくる支援を実施しています。興味がある方は、ぜひサービス紹介ページも覗いてみてください。

1. スタッキング：複数のモデルの出力を新しいモデルの入力に使い、個々のモデルの弱点を補完して予測精度を高める手法。他のアンサンブル学習手法には、バギング（例：RF）やブースティング（例：XGBoost）がある。 ↩︎
2. XGBoost（勾配ブースティング）：決定木を基にした機械学習手法で、多くの木を順次作りながら誤差を修正する。大規模データや非線形データでの高精度な予測が可能で、データ分析コンペなどで広く利用。 ↩︎
3. SVM（サポートベクターマシン）：データを分ける最適な「線」または「面」を見つける分類アルゴリズム。回帰分析にも応用でき、非線形データも高次元空間に変換して処理可能。画像分類などの応用で使われる。 ↩︎
4. RF（ランダムフォレスト）：複数の決定木を用いたアンサンブル学習で、異なるデータサンプルで木を構築することで、安定性と精度が向上。欠損値に強い特徴がある。 ↩︎
5. SHAP（SHapley Additive exPlanations）：ゲーム理論に基づく手法で、モデルの各特徴量が予測に与える影響を数値化・可視化する。個別のサンプルごとの貢献度が明確に示され、解釈性の高い分析が可能。 ↩︎
6. Permutation Importance：特徴量の重要度を測る手法で、特定の特徴量をシャッフルしてモデル性能の低下度合いを測ることで、その特徴量の貢献度を評価する。モデル全体での寄与を評価する際に有効。 ↩︎
7. 決定係数R²：モデルがデータをどれだけ説明しているかを示す指標で、1に近いほどモデルの性能が良いことを意味する。主に回帰分析で利用される。 ↩︎